Breadth First Traversal (or Search)

Breadth First Traversal (or Search) for a graph is similar to Breadth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array.

For simplicity, it is assumed that all vertices are reachable from the starting vertex.

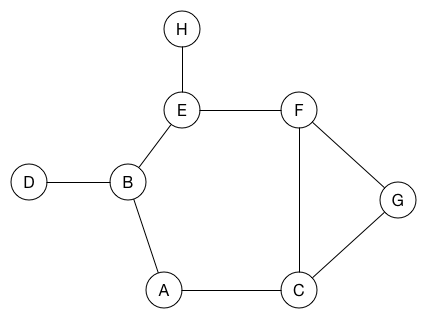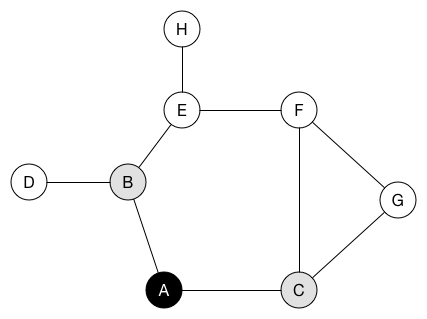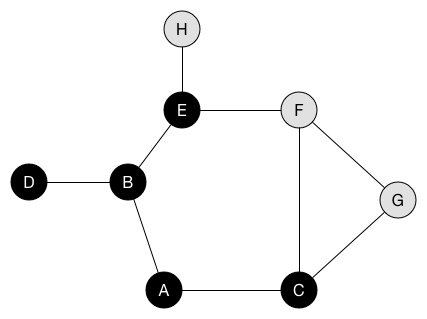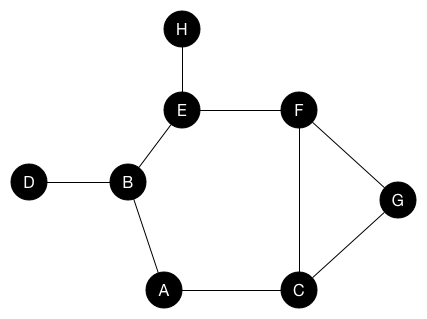
BFS (G, s) // Where G is the graph and s is the root node
      // 1. Inserting s in queue until all its neighbour vertices are marked.
      let Q be queue.
      Q.enqueue( s )

      // 2. Mark
      To mark s as visited.

      // 3. Start traversing
      while ( Q is not empty)
           //Removing that vertex from queue,whose neighbour will be visited now
           v  =  Q.dequeue( )

          //processing all the neighbours of v  
          for all neighbours w of v in Graph G
               if w is not visited
                        Q.enqueue( w ) //Stores w in Q to further visit its neighbour
                        mark w as visited.

void BFS(vector<list<int>> &adjList, int v) {
    auto size = adjList.size();
    vector<bool> visited(size, 0);
    queue<int> q;
    q.push(v);
    visited[v] = true;
    path[v] = 0;

    while (!q.empty()) {
        int n = q.front();
        q.pop();

        for (auto neighbor: adjList[n]) {
            if (visited[neighbor] == false) {
                q.push(neighbor);
            }
        }
        visited[n] = true;
    }
}